body{margin:0;} noscript{z-index: 10000; position: fixed; display: block; height: 100%; width: 100%; background: #fff;} noscript .fa{font-size: 40px; display:block; color: #daa520;} noscript div{margin-top: 6%; padding-left: 20px; padding-right: 20px; text-align: center;} ! Du måste ha JavaScript påslaget för att använda den här webbsidan.

Rekommenderade

Tester

Ett fel uppstod, försök igen senare!

eKurser /

Matematik 1a /

Kapitel {{ article.chapter.number }}

{{ article.number }}.

Visa mindre Visa mer

Inställningar & verktyg för lektion

	{{ 'ml-lesson-number-slides' \| message : article.intro.bblockCount }}
	{{ 'ml-lesson-number-exercises' \| message : article.intro.exerciseCount }}
	{{ 'ml-lesson-time-estimation' \| message }}

Kreditlista Bilder

{{ item.file.title }}
{{ presentation }}

Inga inlägg om filrättigheter hittades

Om man ska rita av något kan det ibland vara oöverskådligt, och i vissa fall omöjligt eller meningslöst, att göra en exakt kopia. Då kan man göra en förminskning eller förstoring. Exempelvis är en karta förminskad jämfört med verkligheten medan en bild på en insekt antagligen är förstorad.

Skala är ett mått på hur mycket man har förminskat eller förstorat. När man talar om skala menar man oftast längdskala, men det finns även area- och volymskala.

Begrepp

Längdskala

En längdskala anger förhållandet mellan längden på en avbildning av ett objekt och objektets verkliga längd. Den kan definieras på följande sätt.

$L \ddot{a} ngdskala = \frac{L a ¨ ngd i avbildning}{Motsvarande l a ¨ ngd i verkligheten}$

Om längdskalan t.ex. är $\frac{1}{4}$ innebär det alltså att avbildningen är en fjärdedel så lång som det verkliga objektet.

Begrepp

Area- och volymskala

Man kan även avgöra hur arean eller volymen i en avbildning förhåller sig till arean eller volymen av det verkliga objektet. Då talar man istället om areaskala respektive volymskala. De definieras på liknande sätt som längdskala.

$Areaskala = \frac{Area i avbildning}{Motsvarande area i verkligheten}$

$Volymskala = \frac{Volym i avbildning}{Motsvarande volym i verkligheten}$

Notation

Skala

Ett vanligt sätt att ange längd-, area- eller volymskala är genom att använda ett kolon. Följande majblomma, som i verkligheten är $4$ cm hög, är t.ex. avbildad i längdskalan $1 : 4$ vilket betyder samma sak som $\frac{1}{4} .$ Skalan utläses ett till fyra och betyder att $1$ cm på bilden motsvarar $4$ cm i verkligheten.

Generellt gäller det att längden i avbildningen anges till vänster om kolonet och motsvarande längd i verkligheten till höger om kolonet.

$Avbildning : Verklighet$

Även för area- och volymskala anges värdena för avbildningen till vänster om kolonet och de verkliga värdena till höger. Om talet till vänster är lägre än det till höger är avbildningen en förminskning medan det är en förstoring om om det vänstra talet är större än det högra.

Bestäm den verkliga längden med skala

fullscreen

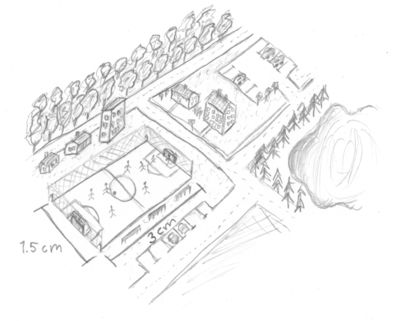
Nike är konstnär och har utmanat sig själv genom att rita av sitt bostadsområde under en helikoptertur.

Hennes fru är matematiker och har kommit fram till att längdskalan mellan Nikes avbildning och verkligheten är $1 : 3000 .$ Använd denna skala för att bestämma de verkliga längderna på fotbollsplanens sidor.

Visa Lösning

Vi vet att skalan är

1 : 3000 .

Det betyder att

1

cm på bilden motsvarar

3000

cm i verkligheten. I skissen ser vi att fotbollsplanens kortsida är

1.5

cm och att långsidan är

3

cm. Vi multiplicerar dessa längder med

3000

för att bestämma hur långa planens sidor är i verkligheten.

Kortsida : 1.5 \cdot 3000 = 4500 cm L \overset{˚}{a} ngsida : 3 \cdot 3000 = 9000 cm

Till sist skriver vi om längderna till enheten meter, eftersom det är mer användbart i sammanhanget. Det gör vi genom att dividera med

100 .

Vi får då att kortsidan är

45

m lång och att långsidan är

90

m lång.

Bestäm skalan

fullscreen

En röd blodkropp har diametern $8$ mikrometer. I en lärobok förstoras en bild på den upp så att diametern blir $4$ cm. Vad blir skalan på avbildningen?

Visa Lösning

Vi beräknar skalan genom att dividera längden på avbildningen med den verkliga längden. Men eftersom längderna är i olika enheter måste vi först skriva om dem till samma, t.ex. meter.

1

mikrometer är en miljondels meter vilket betyder att

8 mikrometer = 8 \cdot 1 0^{- 6} m .

Det går

100

cm på en meter så

4

cm är

\frac{4}{1 0 0} = 0.04

meter. Nu kan vi bestämma skalan.

Skala = \frac{L a ¨ ngd i avbildning}{L a ¨ ngd i verkligheten}

SubstituteValues

Sätt in värden

Skala = \frac{0 . 0 4}{8 \cdot 1 0 ^{- 6}}

UseCalc

Slå in på räknare

Skala = 5000

5000

kan skrivas som ett bråk med nämnaren

1

5000 = \frac{5 0 0 0}{1} .

Detta betyder att skalan är 5000 till 1, vilket brukar skrivas

5000 : 1 .

Laddar innehåll

{{ article.displayTitle }}

Notation

Exempel

Bestäm den verkliga längden med skala

Exempel

Bestäm skalan